多路归并排序中使用的胜者树是从堆排序的堆进化出来的,并进一步发展出了败者树。下面简单分析一下几者的区别。
满二叉树(Full Binary Tree)
满二叉树:除了叶子节点外所有节点都有两个孩子。
完全二叉树(Complete Binary Tree)
完全二叉树:只有最下面的两层结点度能够小于2,并且最下面一层的结点都集中在该层最左边的若干位置的二叉树。
如何用顺序存储表示一棵完全二叉树?
设有节点,其位于第n层(从根到叶,根层编号为0),第k个(从左到右,最左边编号为0);因此n和k也可以理解为其之前的节点层数/节点个数。设其偏移量函数为P(n,k)。
那么我们知道在之前有n层,每层i都是满的,有$2^i$个节点。
$P(n,k)=2^0+2^1+…+2^{n-1}+k$
等比数列求和易得,$P(n,k)=2^n+k-1$。
好,那么该节点的孩子的编号的,层数肯定是n+1,该节点之前的节点都有两个孩子,所以孩子的行编号必然是$2 *k$和$2 *k + 1$。 也就是P(n+1, 2 *k)和P(n+1, 2 *k + 1)
$P(n+1, 2 * k)=2^{n+1}+2k-1=2 * (2^n+k-1)+1=2 * P(n,k)+1$ $P(n+1, 2 * k + 1)=2^{n+1}+2k=2 * (2^n+k-1)+2=2 * P(n,k)+2$
于是我们知道一个节点,如果其偏移量为d,则其子节点的偏移量为2 *d + 1和2 *d + 2。
反过来推算,很容易知道其父节点的偏移量为 (d-1)/2。
二叉堆(Binary Heap)
二叉堆就是一棵完全二叉树,父节点的键值总是小于(或大于)任何一个子节点的键值,且每个节点的左子树和右子树都是一个二叉堆。
- 当父节点的键值总是大于或等于任何一个子节点的键值时为最大堆。 当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆。
应用
堆排序
多路归并排序
二叉堆除了可以应用于对一个数组进行堆排序以外,还可以应用于多路归并排序中。
- 堆排序的后半部分算法中,就是一个很明确的“多个值中选取极值,取出该极值,更新根、然后修复堆”的过程。在多路归并排序中,每次取出极值后,堆的长度未改变。
- 对堆进行修复时,每层调整都要对三个值(父节点、两个子节点)进行至少两次比较。
- 为了减少比较的消耗,人们就发展出胜者树和败者树来。
- 胜者树和败者树都是完全二叉树,是树形选择排序的一种变型。每个叶子结点相当于一个选手,每个中间结点相当于一场比赛,每一层相当于一轮比赛。
- 不同的是,胜者树的中间结点记录的是胜者的标号;而败者树的中间结点记录的败者的标号。
胜者树(Tournament Tree/Winner Tree)
胜者树让所有参与排序的序列提出的值都作为叶子,然后在其上面补充节点成为完全二叉树,父节点会保存两个子节点比较时的胜者。
- 优点:如果一个节点的值改变了,可以很容易地修改这棵胜者树。只需要沿着从该结点到根结点的路径修改这棵二叉树,而不必改变其他路径的结果。
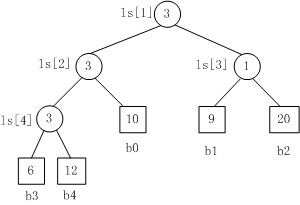
上图是一个胜者树的示例。规定数值小者胜。
- b3 PK b4,b3胜b4负,内部结点ls[4]的值为3;
- b3 PK b0,b3胜b0负,内部结点ls[2]的值为3;
- b1 PK b2,b1胜b2负,内部结点ls[3]的值为1;
- b3 PK b1,b3胜b1负,内部结点ls[1]的值为3。
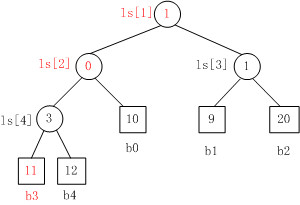
当叶子结点b3的值变为11时,重构的胜者树如Fig. 2所示。
- b3 PK b4,b3胜b4负,内部结点ls[4]的值为3;
- b3 PK b0,b0胜b3负,内部结点ls[2]的值为0;
- b1 PK b2,b1胜b2负,内部结点ls[3]的值为1;
- b0 PK b1,b1胜b0负,内部结点ls[1]的值为1。
败者树(Loser Tree)
败者树和胜者树的结构基本一致,只是父节点保存的不是胜者而是败者,并且额外有个指针保存当前的胜者(修正完毕后自然就是最后胜者了)。
- 在败者树中,用父结点记录其左右子结点进行比赛的败者,而让胜者参加下一轮的比赛。败者树的根结点记录的是败者,需要加一个结点来记录整个比赛的胜利者。采用败者树可以简化重构的过程。
- 优点:败者树的重构只需要与其父结点比较,而胜者树则需要和兄弟节点比较,然后把胜者付赋给父节点。
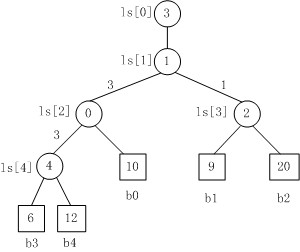
上图是一棵败者树。规定数大者败。
- b3 PK b4,b3胜b4负,内部结点ls[4]的值为4;
- b3 PK b0,b3胜b0负,内部结点ls[2]的值为0;
- b1 PK b2,b1胜b2负,内部结点ls[3]的值为2;
- b3 PK b1,b3胜b1负,内部结点ls[1]的值为1;
- 在根结点ls[1]上又加了一个结点ls[0]=3,记录的最后的胜者。
败者树重构过程如下:
- 将新进入选择树的结点与其父结点进行比赛:将败者存放在父结点中;而胜者再与上一级的父结点比较。
- 比赛沿着到根结点的路径不断进行,直到ls[1]处。把败者存放在结点ls[1]中,胜者存放在ls[0]中。
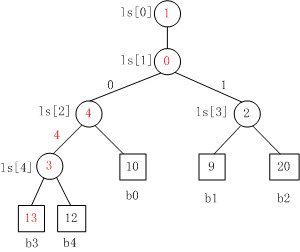
当叶子结点b3变为13时,败者树的重构图。