数组的排序算法有很多,本文对常用的排序算法做了一下总结,并用Java实现(默认从小到大)。
简要比较

- 均按从小到大排列
- k代表数值中的”数位”个数
- n代表数据规模
- m代表数据的最大值减最小值
交换排序
冒泡排序
原理
冒泡排序是一种简单的排序算法。它每次去从开始去比较相邻的两个元素,如果顺序错误就交换过来,当比较到最后一个元素时,就会把最小(最大)的元素找出来;然后再重复比较,前面已经找到的就不再参与比较。元素越小(大)的元素会经过交换慢慢“浮”到数列顶端。
public static void bubbleSort(int[] array) {
if (array == null || array.length <= 1) {
return;
}
//i为无序区长度
for (int i = array.length; i >= 0; i--) {
for (int j = 1; j < i; j++) {
if (array[j - 1] > array[j]) {
swap(array, j - 1, j);
}
}
}
}
快速排序
基本思想:设当前待排序的无序区为R[low..high],利用分治法可将快速排序的基本思想描述为:
- 分解
- 在R[low..high]中任选一个记录作为基准(Pivot),将当前无序区划分为左、右两个较小的子区间,并使左边子区间中所有记录的关键字均小于等于基准记录(不妨记为pivot)的关键字pivot.key,右边的子区间中所有记录的关键字均大于等于pivot.key,而基准记录pivot则位于正确的位置(pivotpos)上,它无须参加后续的排序。
- 划分的关键是要求出基准记录所在的位置
- 求解
public static void quickSort(int[] array) {
if (array == null || array.length <= 1) {
return;
}
partition(array, 0, array.length - 1);
}
private static void partition(int[] array, int low, int high) {
if (low >= high) {
return;
}
int i = low;
int j = high;
int key = array[i];
while (i < j) {
while (i < j && array[j] > key) j--;
if (i < j) array[i++] = array[j];
while (i < j && array[i] < key) i++;
if (i < j) array[j--] = array[i];
}
array[i] = key;
partition(array, low, i - 1);
partition(array, i + 1, high);
}
- 优化
- 三数取中
- 取partition的low、mid、high中的中位数作为基准
- 插排
- 当high-low<10时,使用直接插入排序,对于小数组,快排比插入排序要慢;
- 聚集相等元素
- 保存4个索引,将与key(基准值)不相等的元素逐渐交换到数组的两端,最后对中间区域进行赋值为key。
- 三数取中
插入排序
直接插入排序
原理
通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
代码
public static void insertSort(int[] array) {
if (array == null || array.length <= 1) {
return;
}
for (int i = 1; i < array.length; i++) {
int key = array[i];
int j = i - 1;
while (j >= 0 && array[j] > key) {
array[j + 1] = array[j];
j--;
}
array[j + 1] = key;
}
}
性能分析
- 复杂度分析:
- 平均来说,插入排序的复杂度为O($n^2$);
- 最好的情况:已经有序,只需要比较操作N−1次即可;
- 最坏的情况:逆序,需要比较N∗(N−1)/2次。
- 特点:
- 插入排序很适合部分有序的数组和规模较小的数组;
- 插入排序不适合对于数据量比较大的排序应用。
- 对于单链表排序,插入排序性能最优(移动操作减少)。
折半插入排序(二分查找排序)
在有序区中利用二分查找搜索key的插入位置。
public static void binaryInsertSort(int[] array) {
if (array == null || array.length <= 1) {
return;
}
for (int i = 1; i < array.length; i++) {
int key = array[i];
int low = 0;
int high = i - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (array[mid] >= key) {
high = mid - 1;
} else {
low = mid + 1;
}
}
for (int j = i - 1; j > high; j--) {
array[j + 1] = array[j];
}
array[high + 1] = key;
}
}
希尔排序
希尔排序的实质就是分组插入排序。
-
因为直接插入排序在元素基本有序的情况下(接近最好情况),效率是很高的,因此希尔排序在时间效率上比冒泡排序和直接插入排序有较大提高。
-
基本思想是:先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序(此时增量为1)。
public static void shellSort(int[] array) {
if (array == null || array.length <= 1) {
return;
}
for (int increment = array.length / 3 + 1; increment > 0; increment /= 3) {
for (int i = increment; i < array.length; i++) {
int key = array[i];
int j = i - increment;
while (j >= 0 && array[j] > key) {
array[j + increment] = array[j];
j -= increment;
}
array[j + increment] = key;
}
}
}
性能分析
- 复杂度分析:步长的设置,影响着希尔排序算法的复杂度,具体可参考维基百科之希尔排序,这里给出一个步长序列与复杂度的关系表:
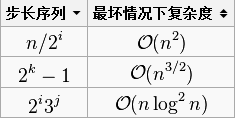
- 特点
- 排序最重要的地方在于当用较小步长排序后,以前用的较大步长仍然是有序的。比如,如果一个数列以步长5进行了排序然后再以步长3进行排序,那么该数列不仅是以步长3有序,而且是以步长5有序。
选择排序
直接选择排序
原理
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
代码
public static void selectSort(int[] array) {
if (array == null || array.length <= 1) {
return;
}
for (int i = array.length - 1; i > 0; i--) {
int max = 0;
int j = 1;
while (j <= i) {
if (array[j] > array[max]) {
max = j;
}
j++;
}
swap(array, max, i);
}
}
性能分析
- 复杂度分析:
- 对于长度为N的数组,选择排序需要大约$N^2/2$次比较和N次交换;
- 最好的情况:已经有序,交换0次;
- 最坏的情况:逆序,交换N−1次。
- 特点:
- 运行时间与输入无关,即使对于一个有序数组,依然需要扫描全部元素而且运行时间与随机数组一样;
- 数据移动是最少的。交换次数与数组大小成线性关系。
堆排序
public static void heapSort(int[] array) {
if (array == null || array.length <= 1) {
return;
}
for (int i = array.length / 2; i >= 0; i--) {
maxHeapify(array, i, array.length);
}
for (int i = array.length; i > 0; i--) {
swap(array, 0, i - 1);
maxHeapify(array, 0, i - 1);
}
}
private static void maxHeapify(int[] array, int i, int heapSize) {
int min = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
if (left < heapSize && array[left] > array[min]) min = left;
if (right < heapSize && array[right] > array[min]) min = right;
if (min != i) {
swap(array, i, min);
maxHeapify(array, min, heapSize);
}
}
归并排序
public static void mergeSort(int[] array) {
if (array == null || array.length <= 1) {
return;
}
mergeSortHelper(array, 0, array.length-1);
}
private static void mergeSortHelper(int[] array, int low, int high) {
if (low < high) {
int mid = low + (high - low) / 2;
mergeSortHelper(array, low, mid);
mergeSortHelper(array, mid + 1, high);
merge(array, low, mid, high);
}
}
private static void merge(int[] array, int low, int mid, int high) {
int[] tempArray = new int[high - low + 1];
int i = low;
int j = mid + 1;
int k = 0;
while (i <= mid && j <= high) {
if (array[i] < array[j]) {
tempArray[k++] = array[i++];
} else {
tempArray[k++] = array[j++];
}
}
while (i <= mid) {
tempArray[k++] = array[i++];
}
while (j <= high) {
tempArray[k++] = array[j++];
}
k = low;
for (int temp : tempArray) {
array[k++] = temp;
}
}